Category:Permutohedron of order 4 (raytraced)
Permutohedron vs. Cayley graph edit
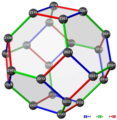
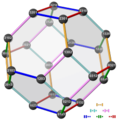
The two truncated octahedra below are the permutohedron of the symmetric group S4 and one of its Cayley graphs,
namely the one generated by the 3 transpositions that swap neighbouring elements.
(The 3 permutations connected to the lowest vertex.)
The solid has 24 vertices and 36 edges. The vertices are the 24 permutations of .
In the permutohedron they make sense as coordinates in a 3D hyperplane of 4D space. Those in the Cayley graph are their inverses.
In both figures higher permutations are more out of order than those below.
(The lowest vertex is in natural order, and the highest is its reversal.)
And in both figures permutations connected by an edge differ in exactly two places. The edge color indicates which places.
(In both figures a green edge indicates that the two places in the middle are swapped.
In the permutohedron an ochre edge indicates that the first and last are swapped.)
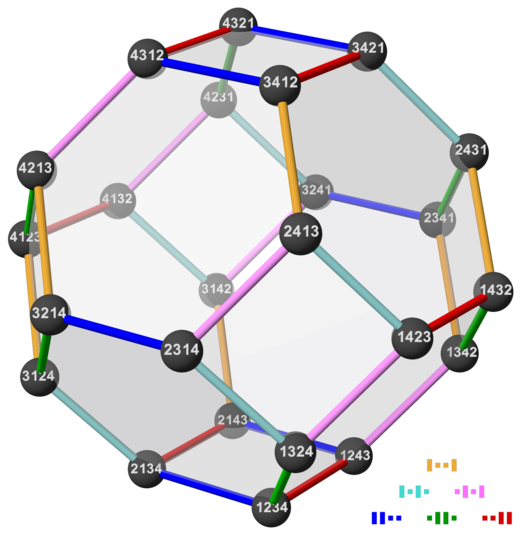
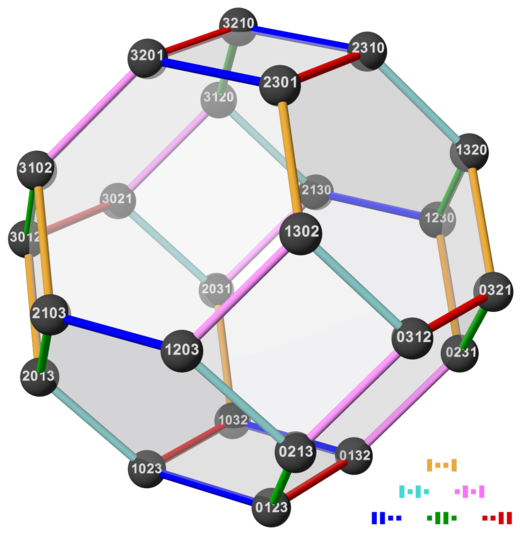
| In the | permutohedron | the swapped | values | are next to each other (no matter how far the | places | are apart). E.g. the | values | 3 and 4 in the edge from (2, 3, 1, 4) to (2, 4, 1, 3). |
| In the | Cayley graph | the swapped | places | are next to each other (no matter how far the | values | are apart). E.g. the | places | 3 and 4 in the edge from (3, 1, 2, 4) to (3, 1, 4, 2). |
The edges have 6 different directions (corresponding to the edges of a tetrahedron).
In the permutohedron parallel edges have the same color. There are 6 edges of each direction.
The Cayley graph has only 3 edge colors, and each vertex has one edge of every color. (There are 12 edges of each color. Two edges of each color are parallel.)
The permutohedron is the Hasse diagram of the weak order of permutations. (The neutral permutation and its reversal are its least and greatest elements.)
So the permutohedron can be seen as directed. The Cayley graph is undirected, because all generators are transpositions (and thus self-inverse).
 |
 |
 |
| numbered vertices | ||
|---|---|---|
|
In the two solids shown below, the vertices are labeled with the index numbers of the permutations. The style of each node indicates the conjugacy class. | ||
 |
 |
 |
| order 3 | ||
|---|---|---|
 |
 |
 |
Permutohedron in simplex edit
(Unlike the section above, this one uses 0-based permutations.)
The 24 permutations can be seen a coordinates of points, and the permutohedron as the convex hull of these points.
They are in the same hyperplane, defined by the sum of coordinates. For permutations of the sum is . (3rd triangular number)
An interesting subsection of this hyperplane is the simplex that intersects with the first orthant, i.e. the points with non-negative coordinates.
The image on the left shows the integer points in that section. Their number is the figurate number . (7th tetrahedral number)
The section above described that two permutohedron vertices connected by an edge differ only in two places.
In this section it can be seen that all points differ only in two places if they are both on a parallel to a tetrahedron edge.
E.g. these six points are on one line that contains a permutohedron edge:
(1, 0, 0, 5),
(1, 1, 0, 4),
(1, 2, 0, 3),
(1, 3, 0, 2),
(1, 4, 0, 1),
(1, 5, 0, 0)
 |
 |
 |
| order 3 | ||
|---|---|---|
|
For permutations of the sum is . (2nd triangular number) | ||
 |
 |
 |
Media in category "Permutohedron of order 4 (raytraced)"
The following 12 files are in this category, out of 12 total.
-
Permutohedron in simplex of order 4 (0-based).png 3,740 × 4,000; 1.98 MB
-
Permutohedron in simplex of order 4 (1-based).png 3,740 × 4,000; 1.98 MB
-
Permutohedron in simplex of order 4, with truncated tetrahedron (0-based).png 3,740 × 4,000; 2.21 MB
-
Permutohedron in simplex of order 4, with truncated tetrahedron (1-based).png 3,740 × 4,000; 2.21 MB
-
Symmetric group 4; Cayley graph 1,2,6 (0-based).png 3,900 × 4,000; 1.08 MB
-
Symmetric group 4; Cayley graph 1,2,6 (1-based).png 3,900 × 4,000; 1.07 MB
-
Symmetric group 4; permutohedron 3D; transpositions (0-based).png 3,900 × 4,000; 1.37 MB
-
Symmetric group 4; permutohedron 3D; transpositions (1-based).png 3,900 × 4,000; 1.36 MB
-
Tetrahedron with colored edges a.png 2,631 × 2,856; 662 KB
-
Tetrahedron with colored edges b.png 2,631 × 2,856; 670 KB
-
Tetrahedron with colored edges, labeled.png 2,835 × 3,000; 785 KB
-
Tetrahedron with colored edges.png 2,835 × 3,000; 655 KB