File:Academ Platonic icosahedron from its dual.svg

Original file (SVG file, nominally 950 × 760 pixels, file size: 4 KB)
Captions
Captions
Summary edit
| DescriptionAcadem Platonic icosahedron from its dual.svg |
English: A Platonic dodecahedron has twelve faces. A given face is adjacent to five faces. Five planes contain these five faces: they expand infinitely the five faces. The five planes intersect at a point on the axis of the given face, and on five straight lines expanding five edges of the dodecahedron. Thus, twelve points are created from a Platonic dodecahedron, which are twelve vertices of a Platonic icosahedron. The two solids are called dual polyhedra. Here they are concentric: their two circumscribed spheres have the same center. Both have thirty edges. One of them has as many faces as the other one has vertices: twelve or twenty.
Denoted by The sight direction is the same in this other image of dodecahedron. The figure is yielded through an orthogonal projection onto a plane. The direction of this projection is parallel to a straight line passing through two opposite vertices of the dodecahedron, also parallel to the common axis of two opposite faces of the icosahedron. Hence the drawing does not distort these two opposite faces. Depicted with dashed lines, the three sides of one of these two equilateral triangles are partly masked by the dodecahedron. None of the edges of the dodecahedron is dashed, its nine hidden edges are not represented. Another planar projection transforms ten vertices of the icosahedron into vertices of regular decagons — a given regular decagon is either stellated or convex —. Given a convex regular polygon or a convex regular polyhedron, we can build a new regular object by extending all the sides of the polygon or all the faces of the polyhedron, provided that the extensions intersect. This process is called a "stellation" of the initial object. Thus we build five sides of a stellated regular pentagon by extending five green edges of the dodecahedron. Among the twelve stars with five branches in the twelve face planes of the dodecahedron, only two stars are depicted. Each face plane of the dodecahedron contains such a star with five branches, of which the vertices are five vertices of the icosahedron. Actually, some cross sections of the icosahedron are faces of a "great dodecahedron", which shares its edges with the icosahedron. Four special blue lines are shrunk images of four sides of such a cross section of the icosahedron, that is a duplicate of a face of the dodecahedron to scale φ 2, or (φ + 1). Depicted by an ordinary blue line, the fifth side of the convex regular pentagon has its real length through the representation. Similarly, four special green lines are shrunk images of four sides of a face of the dodecahedron. The representation preserves the fifth side length. Whatever the sense of the rotation, one third of one turn around the axis of a face of the icosahedron transforms the Platonic solids into themselves. The outline of the icosahedron is a regular hexagon. The side length of this hexagon is not the edge length of the icosahedron. But the representation preserves the distance between two opposite edges, if the two edges are depicted in the outline of the icosahedron. This distance equals φ : two opposite edges of a Platonic icosahedron are two smaller sides of a golden rectangle. : two opposite edges of a Platonic icosahedron are two smaller sides of a golden rectangle.Français : Un dodécaèdre de Platon a douze faces. Une face donnée est adjacente à cinq faces. Cinq plans contiennent ces cinq faces : ils prolongent à l’infini les cinq faces. Les cinq plans se coupent en un point situé sur l’axe de la face donnée, et sur cinq droites qui prolongent cinq arêtes du dodécaèdre. Ainsi, douze points sont créés à partir d’un dodécaèdre de Platon, qui sont douze sommets d’un icosaèdre de Platon. Les deux solides sont appelés des polyèdres duaux. Ici, ils sont concentriques : leurs deux sphères circonscrites ont le même centre. Tous les deux ont trente arêtes. L’un d’eux a autant de faces que l’autre a de sommets : douze ou vingt.
Notée La direction de la vue est la même dans cette autre image d’un dodécaèdre. La figure résulte d’une projection orthogonale sur un plan. La direction de cette projection est parallèle à une droite passant par deux sommets opposés du dodécaèdre, également parallèle à l’axe commun de deux faces opposées de l’icosaèdre. Donc, la perspective ne déforme pas ces deux faces opposées. Représentés en pointillés, les trois côtés de l’un de ces deux triangles équilatéraux sont masqués en partie par le dodécaèdre. Aucune des arêtes du dodécaèdre n’est en pointillé, ses neuf arêtes cachées ne sont pas représentées. Une autre projection plane transforme dix sommets de l’icosaèdre en dix sommets de décagones réguliers — un décagone régulier donné est soit étoilé, soit convexe —. Étant donné un polygone régulier convexe ou un polyèdre régulier convexe, on peut construire un nouvel objet régulier en prolongeant tous les côtés du polygone ou toutes les faces du polyèdre, pourvu que les prolongements se coupent. Ce procédé s’appelle “étoiler” l’objet initial. Ainsi nous contruisons cinq côtés d’un pentagone régulier étoilé en prolongeant cinq arêtes vertes du dodécaèdre. Parmi les douze étoiles à cinq branches contenues dans les douze plans des faces du dodécaèdre, seulement deux étoiles sont représentées. Chaque plan d’une face du dodécaèdre contient une telle étoile à cinq branches, dont les sommets sont cinq sommets de l’icosaèdre. En effet, certaines sections planes de l’icosaèdre sont des faces d’un “grand dodécaèdre”, qui a les mêmes arêtes que l’icosaèdre. Quatre lignes bleues spéciales sont des images rétrécies de quatre côtés d’une telle section, qui est une réplique d’une face du dodécaèdre à l'échelle φ 2, ou (φ + 1). Représenté par une ligne bleue ordinaire, le cinquième côté du pentagone régulier convexe est en vraie grandeur dans la représentation. De la même façon, quatre lignes vertes spéciales sont des images rétrécies de quatre côtés d’une face du dodécaèdre. La perspective respecte la longueur du cinquième côté. Quel que soit le sens de la rotation, un tiers de tour autour de l’axe d’une face de l’icosaèdre transforme les deux solides de Platon en eux-mêmes. Le contour de l’icosaèdre est un hexagone régulier. La longueur d’un côté de cet hexagone n’est pas la longueur d’une arête de l’icosaèdre. Mais la perspective représente en vraie grandeur la distance entre deux arêtes opposées, si les deux arêtes sont représentées sur le contour de l’icosaèdre. Cette distance est égale à φ : deux arêtes opposées d’un icosaèdre de Platon sont deux petits côtés d’un rectangle d’or. : deux arêtes opposées d’un icosaèdre de Platon sont deux petits côtés d’un rectangle d’or. |
| Date | |
| Source | Own work |
| Author | Baelde |
| Other versions |
 |
| SVG development InfoField | This /Baelde was created with a text editor. |
Licensing edit
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
- share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

|
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 10:55, 23 December 2012 |  | 950 × 760 (4 KB) | Baelde (talk | contribs) | adding two equalities in an improved image |
| 14:16, 29 March 2012 | 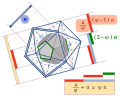 | 950 × 760 (4 KB) | Baelde (talk | contribs) | some lines more thick | |
| 09:24, 20 March 2012 | 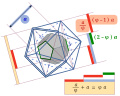 | 950 × 760 (4 KB) | Baelde (talk | contribs) | Better draw attention to some stellations | |
| 13:15, 17 March 2012 |  | 950 × 760 (4 KB) | Baelde (talk | contribs) | correct aspect ratio | |
| 13:15, 17 March 2012 |  | 800 × 640 (4 KB) | AnonMoos (talk | contribs) | correct proportions | |
| 12:05, 17 March 2012 |  | 760 × 950 (4 KB) | Baelde (talk | contribs) | without title | |
| 09:43, 17 March 2012 |  | 760 × 950 (4 KB) | Baelde (talk | contribs) | {{Information |Description ={{en|1=A Platonic dodecahedron has twelve faces. A given face is adjacent to five faces. Five planes con... |
You cannot overwrite this file.
File usage on Commons
The following 2 pages use this file:
File usage on other wikis
The following other wikis use this file:
- Usage on en.wikipedia.org
Metadata
This file contains additional information such as Exif metadata which may have been added by the digital camera, scanner, or software program used to create or digitize it. If the file has been modified from its original state, some details such as the timestamp may not fully reflect those of the original file. The timestamp is only as accurate as the clock in the camera, and it may be completely wrong.
| Width | 950 |
|---|---|
| Height | 760 |