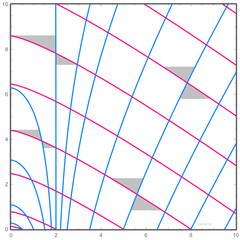
DescriptionSchwarzschild-Droste-Space-Time-Vectors-Of-Outgoing-Null-Congruences.png	Deutsch: Vektorplot der Schwarzschild Raumzeit in Schwarzschild Droste Koordinaten. Ausgehende Photonen (v=+c). x=r, y=t
Date	29 November 2022
Source	Own work → Link
Author	Yukterez (Simon Tyran, Vienna)
Other versions

I, the copyright holder of this work, hereby publish it under the following license:

This file is licensed under the Creative Commons Attribution-Share Alike 4.0 International license.

You are free:

• to share – to copy, distribute and transmit the work
• to remix – to adapt the work

Under the following conditions:

• attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
• share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

https://creativecommons.org/licenses/by-sa/4.0CC BY-SA 4.0 Creative Commons Attribution-Share Alike 4.0 truetrue

• 
  A1) Schwarzschild Droste
• 
  A2) Gullstrand Painlevé
• 
  A3) Eddington Finkelstein

• 
  B1) Schwarzschild Droste
• 
  B2) Gullstrand Painlevé
• 
  B3) Eddington Finkelstein

• 
  C1) Schwarzschild Droste
• 
  C2) Gullstrand Painlevé
• 
  C3) Eddington Finkelstein

• 
  D1) SD, ingoing lightlike vectors
• 
  D2) SD, outgoing lightlike vectors
• 
  D3) EF, ingoing timelike vectors

• 
  E1) Schwarzschild Droste
• 
  E2) Gullstrand Painlevé
• 
  E3) Eddington Finkelstein

In Gullstrand Painlevé coordinates the local observers (or clocks and rulers) who define the direction of the space and time axes are free falling raindrops with the negative escape velocity ${\displaystyle {\rm {v=-\surd [2/r]}}}$ (relative to local observers stationary with respect to the black hole), while in Eddington Finkelstein coordinates they are accelerating to the squared raindrop velocity ${\displaystyle {\rm {v=-2/r}}}$, which they achieve by a proper acceleration of ${\displaystyle {\rm {a=F/m=1/\surd [(r+2)^{3}r]}}}$ radially outwards, so de facto a deceleration. In the classic Schwarzschild Droste coordinates the local clocks and rulers are stationary with respect to the black hole, so they also experience a proper outward acceleration of ${\displaystyle {\rm {a=1/r^{2}/\surd [1-2/r]}}}$, which is infinite at ${\displaystyle {\rm {r=2}}}$.

In SD and GP coordinates, ingoing and outgoing worldlines at ${\displaystyle {\rm {r\to 0}}}$ terminate with infinite coordinate velocity ${\displaystyle {\rm {dr/dt\to -1/0}}}$ (therefore around ${\displaystyle {\rm {r=0}}}$ they are depicted as horizontal worldlines on the spacetime diagrams), while in EF coordinates they arrive with ${\displaystyle {\rm {dr/dt=-1}}}$, which holds for timelike and lightlike geodesics (they all have ${\displaystyle 45\mathrm {{}^{\circ }} }$ at ${\displaystyle {\rm {r\to 0}}}$ on the diagrams). The local velocity of photons relative to other local infalling test particles and the singularity is ${\displaystyle {\rm {v=\pm 1}}}$ though all the way, while the velocity of timelike test particles goes to ${\displaystyle {\rm {v\to -\infty }}}$ relative to the singularity.

With the Schwarzschild Droste line element

${\displaystyle {\rm {ds^{2}=g_{tt}\ dt^{2}+g_{rr}\ dr^{2}=(1-2/r)\ dt^{2}-dr/(1-2/r)=0}}}$

we get for lightlike radial paths

${\displaystyle {\rm {{\bar {r}}=dr/dt=\pm (r-2)/r}}}$

therefore the time by radius is

${\displaystyle {\rm {t=\int _{r_{1}}^{r_{2}}dr/{\bar {r}}=\pm (r_{1}+r_{2}-2\ln(r_{1}-2)+2\ln(r_{2}-2))}}}$

With the Gullstrand Painlevé line element

${\displaystyle {\rm {ds^{2}=g_{tt}\ dt^{2}+g_{rr}\ dr^{2}+2g_{tr}\ dt\ dr=(1-2/r)\ dt^{2}-dr-{\sqrt {8/r}}\ dr\ dt=0}}}$

we get for lightlike radial paths

${\displaystyle {\rm {{\bar {r}}=dr/dt=-1-{\sqrt {2/r}}\ ||\ 1-{\sqrt {2/r}}}}}$

therefore the time by radius is

${\displaystyle {\rm {t=\int _{r_{1}}^{r_{2}}dr/{\bar {r}}=r_{1}-2{\sqrt {2}}{\sqrt {r_{1}}}+4\ln \left({\sqrt {r_{1}}}+{\sqrt {2}}\right)-r_{2}+2{\sqrt {2}}{\sqrt {r_{2}}}-4\ln \left({\sqrt {r_{2}}}+{\sqrt {2}}\right)}}}$

for ingoing, and for outgoing rays

${\displaystyle {\rm {t=-r_{1}-2{\sqrt {2}}{\sqrt {r_{1}}}-2\ln(r_{1})-4\ln \left(1-{\sqrt {2/r_{1}}}\right)+r_{2}+2{\sqrt {2}}{\sqrt {r_{2}}}+2\ln(r_{2})+4\ln \left(1-{\sqrt {2/r_{2}}}\right)}}}$

With the Eddington Finkelstein line element

${\displaystyle {\rm {ds^{2}=g_{tt}\ dt^{2}+g_{rr}\ dr^{2}+2g_{tr}\ dt\ dr=(1-2/r)\ dt^{2}-(1+2/r)\ dr-4/r\ dr\ dt=0}}}$

we get for lightlike radial paths

${\displaystyle {\rm {{\bar {r}}=dr/dt=-1\ ||\ (r-2)/(r+2)}}}$

therefore the time by radius is

${\displaystyle {\rm {t=\int _{r_{1}}^{r_{2}}dr/{\bar {r}}=r_{1}-r_{2}}}}$

for ingoing, and for outgoing rays

${\displaystyle {\rm {t=-r_{1}-4\ln(r_{1}-2)+r_{2}+4\ln(r_{2}-2)}}}$

For the escape velocity we set ${\displaystyle {\rm {E=-p_{r}=g_{tt}\ dt/ds=1}}}$ and for photons ${\displaystyle {\rm {ds=0}}}$, then solve for ${\displaystyle {\rm {dr/dt}}}$.

In Droste coordinates we get

${\displaystyle {\rm {dr/dt=\pm (1-2/r){\sqrt {2/r}}}}}$

for the free falling worldlines with the positive and negative escape velocities.

The local velocity relative to the stationary observers is

${\displaystyle {\rm {v={\frac {dr}{dt}}\ {\sqrt {-{\frac {g_{rr}}{g_{tt}}}}}}}}$

so the time by radius is

${\displaystyle {\rm {\pm t=-{\frac {1}{3}}{\sqrt {2}}\left(r_{1}^{3/2}+6{\sqrt {r_{1}}}-{\sqrt {r_{2}}}(r_{2}+6)\right)+4\ arctanh{\sqrt {2/r_{1}}}-4\ arctanh{\sqrt {2/r_{2}}}}}}$

In Raindrop coordinates we get

${\displaystyle {\rm {{\frac {dr}{dt}}={\frac {r-2}{r+2}}\ {\sqrt {\frac {2}{r}}}\ ||-{\sqrt {\frac {2}{r}}}}}}$

which gives us

${\displaystyle {\rm {t={\frac {1}{3}}{\sqrt {2}}\left(r_{1}^{3/2}-r_{2}^{3/2}\right)\ ||\ -{\frac {1}{3}}{\sqrt {2}}\left(r_{1}^{3/2}+12{\sqrt {r_{1}}}-{\sqrt {r_{2}}}(r_{2}+12)\right)+8\ arctanh{\sqrt {2/r_{1}}}-8\ arctanh{\sqrt {2/r_{2}}}}}}$

In ingoing Eddington Finkelstein coordinates we get

${\displaystyle {\rm {{\frac {dr}{dt}}={\frac {{\sqrt {2}}\ (r-2)}{{\sqrt {8}}\pm r^{3/2}}}}}}$

therefore the time by radius is

${\displaystyle {\rm {t={\frac {1}{3}}{\sqrt {2}}\left(r_{1}^{3/2}+6{\sqrt {r_{1}}}-{\sqrt {r_{2}}}(r_{2}+6)\right)+2\ln \left({\frac {r_{2}-2}{r_{1}-2}}\right)-4\ arctanh{\sqrt {2/r_{1}}}+4\ arctanh{\sqrt {2/r_{2}}}}}}$

for ingoing geodesics, and for outgoing ones

${\displaystyle {\rm {t=-{\frac {1}{3}}{\sqrt {2}}\left(r_{1}^{3/2}+6{\sqrt {r_{1}}}-{\sqrt {r_{2}}}(r_{2}+6)\right)+2\ln \left({\frac {r_{2}-2}{r_{1}-2}}\right)+4\ arctanh{\sqrt {2/r_{1}}}-4\ arctanh{\sqrt {2/r_{2}}}}}}$

With the Schwarzschild Droste line element we get for the local velocity of ${\displaystyle {\rm {v=\pm v_{e}^{2}}}}$:

${\displaystyle {\rm {dr/dt=\pm (2r-4)/r}}}$

With the Gullstrand Painlevé line element we get

${\displaystyle {\rm {dr/dt={\frac {4-2r}{r^{2}-{\sqrt {8r}}}}\ ||\ {\frac {2r-4}{r^{2}+{\sqrt {8r}}}}}}}$

With the Eddington Finkelstein line element

${\displaystyle {\rm {ds^{2}=g_{tt}\ dt^{2}+g_{rr}\ dr^{2}+2g_{tr}\ dt\ dr=(1-2/r)\ dt^{2}-(1+2/r)\ dr-4/r\ dr\ dt}}}$

we get for the local velocity of ${\displaystyle {\rm {v=\pm v_{e}^{2}}}}$:

${\displaystyle {\rm {dr/dt=-{\frac {2}{r+2}}\ ||\ {\frac {2(r-2)}{r^{2}+4}}}}}$

The vectors of the ingoing null conguences in Schwarzschild Droste coordinates are

${\displaystyle {\rm {\{dt,\ dr\}=sign(r-2)\ \{1,\ 2/r-1\}}}}$

The vectors of the outgoing null conguences in Schwarzschild Droste coordinates are

${\displaystyle {\rm {\{dt,\ dr\}=\{1,\ 1-2/r\}}}}$

The vectors of free falling worldlines with the negative and positive escape velocity in Eddington Finkelstein coordinates are

${\displaystyle {\rm {\{dt,\ dr\}=\{1,\ {\sqrt {2}}(r-2)/({\sqrt {8}}\pm r^{3/2})\}}}}$

Here we simply have ${\displaystyle {\rm {t\to t}}}$.

For the Schwarzschild Droste timelines in Raindrop coordinates we have

${\displaystyle {\rm {t\to t-\left({\sqrt {8}}\left({\sqrt {r_{2}}}-{\sqrt {r_{1}}}\right)+4\ arctanh{\sqrt {2/r_{1}}}-4\ arctanh{\sqrt {2/r_{2}}}\right)}}}$

In Eddington Finkelstein coordinates the Schwarzschild Droste bookkeeper timelines are given by

${\displaystyle {\rm {t\to t-\ln \left({\frac {r_{2}^{2}-4}{r_{1}^{2}-4}}\right)}}}$

Natural units of ${\displaystyle {\rm {G=M=c=1}}}$ are used. Code and other coordinates: Source